You might have come across the analogy where a butterfly flaps its wings in Nagoya and a hurricane occurs in South Florida. The basic idea of the Butterfly Effect is that a small change in the initial parameter can significantly affect the later state. In other words, it is sensitively dependent on initial conditions. In fact, for my extended essay, I was going to investigate the double pendulum, another example of a system that is highly dependent on initial conditions. For instance, if the initial position of the pendulum differs by a tiny bit, the trajectory will diverge from that of the default parameter by a significant amount. These are also referred to as chaotic systems.
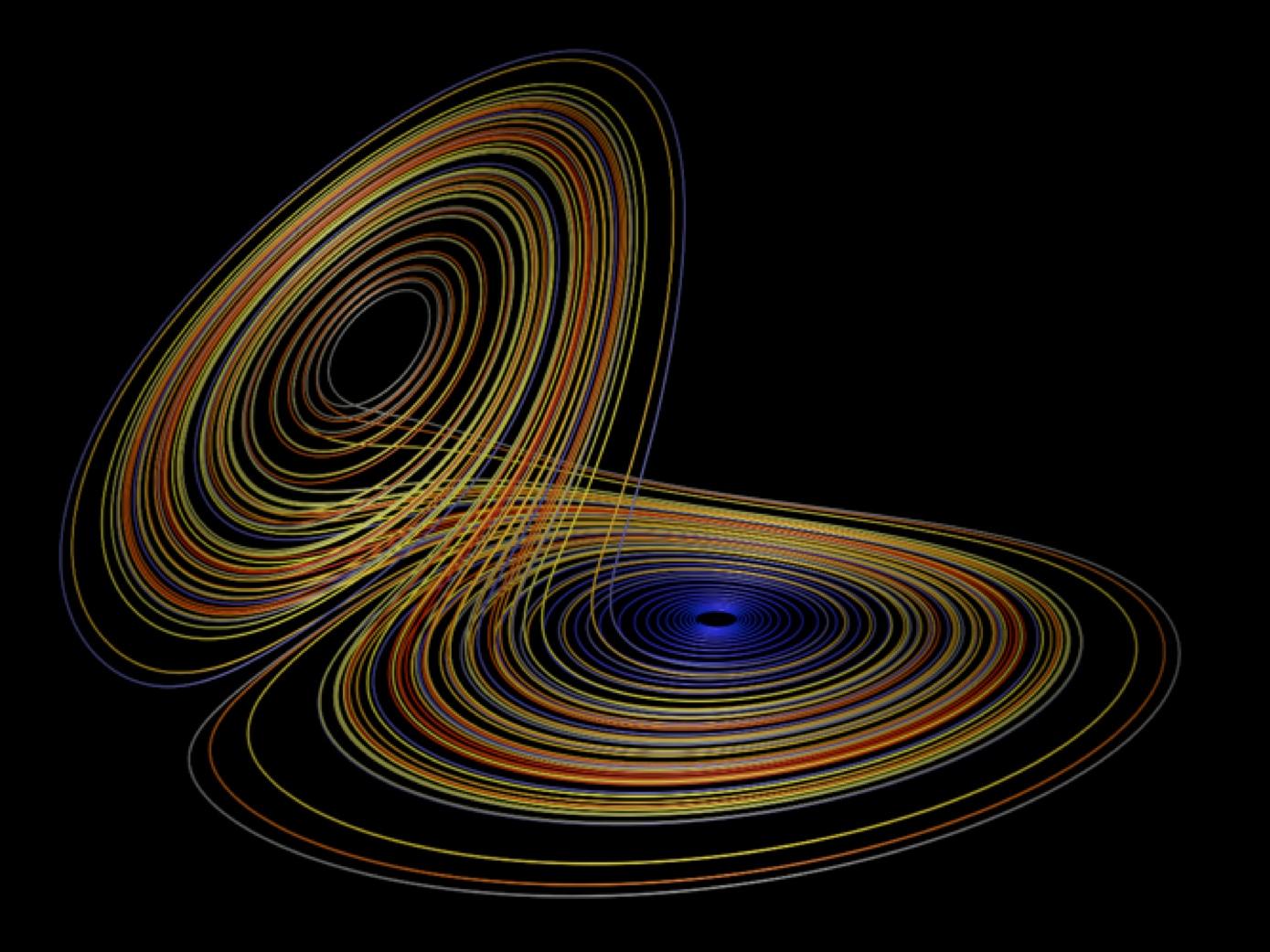
The Lorenz model consists of three ordinary differential equations $$\frac{dx}{dt} = \sigma(y-x)$$ $$\frac{dy}{dt} = x(\rho -z) - y$$ $$\frac{dz}{dt} = xy - βz$$
The variables $\sigma$ , $\rho$, and β are the initial parameters, and if you change these variables in my simulation attached below, you can observe interesting effects. The initial values of these in my simulation are the values that Lorenz used in 1963. In my simulation, I set dx, dy, and dz respectively to the three equations. For each frame, I add these values to x, y, and z, and plot point vector (x, y, z) in p5js.
See the Pen Lorenz Attractor p5.js by steven oh (@stevenohohohohoh) on CodePen.
See the Pen qBqVbVw by steven oh (@stevenohohohohoh) on CodePen.
The double pendulum is, again, a chaotic system that is heavily dependent on its initial parameters, namely the length of the legs, position of the bobs.etc. If you click the codepen icon, you can go to my project page and alter those parameters and test it out! ps. i didn't make this one. Credits to https://editor.p5js.org/codingtrain/sketches/jaH7XdzMK