Reverse Geocoding in Python to Estimate % Land Water on Earth

This is a quick programme I wrote up back in April of 2020 to support my mathematics investigation.

The Code

import random, time
from geopy.geocoders import Nominatim
from geopy.exc import GeocoderTimedOut

NUM_TRIALS = 20
waterCount = 0
geolocator = Nominatim(user_agent="SoySoy4444") #the user_agent can be any string
countryFrequencies = {}

#Recursive function 
def reverseGeocode(location):
    try:
        return geolocator.reverse(location, language="en")
    except GeocoderTimedOut:
        print("Timed out... retrying")
        return reverseGeocode(location)

for i in range(NUM_TRIALS):
    long = random.uniform(-180, 180)
    lat = random.uniform(-90, 90)
    coordinates = "%d, %d" % (lat, long)
    #if you're familiar with fstrings (Python 3.6+), this is the same as f"{lat}, {long}"
    location = reverseGeocode(coordinates)

    if location == None: #must be ocean
        waterCount += 1
        print(i, "\t", lat, "\t", long, "\t", "Water")
    else: #must be land
        try:
            country = location.raw["address"]["country"]
            print(i, "\t", lat, "\t", long, "\t", country)
            if country in countryFrequencies.keys():
                countryFrequencies[country] += 1
            else:
                countryFrequencies[country] = 1
        except KeyError: #Antarctica
            unknownLocation = location.raw["display_name"]
            print(i, "\t", lat, "\t", long, "\t", unknownLocation)
            if unknownLocation in countryFrequencies.keys():
                countryFrequencies[unknownLocation] += 1
            else:
                countryFrequencies[unknownLocation] = 1
    time.sleep(0.2)

print("There were %d water images out of %d images" % (waterCount, NUM_TRIALS))
print("Water %:", waterCount/NUM_TRIALS*100, "%")
print(countryFrequencies)

What it is

My assignment was to estimate the percentage of land water by randomly walking on the surface of the Earth on random.org and manually counting how many of the coordinates were on water!

I instantly thought to myself, "such repetitive, menial tasks are perfect for python!" And so I began researching about the easiest way to accomplish my task.

Initially, I was hopeful that either the Google Maps API or the OpenStreetMap API would have a feature to classify a given geographical coordinate as either land and water, but alas, a few minutes of Googling told me otherwise.

It led me to this post on Stack Overflow, which suggested something called reverse geocoding.

In simple terms, reverse geocoding is the process of converting a given coordinate on the Earth to an address. In this case, the key idea is the fact that a point in the ocean does not have an address .

How it Works

Key library used: Geopy

Geopy is just a collection of different geolocation services bundled together in a library. Nominatim by OpenStreetMap is the geolocation service I used, but there are many other alternatives including Bing and GoogleV3 by Google Maps. Click here to view the full list on the Geopy documentation.

A brief pseudocode:

1. Generate a random coordinate
2. Reverse geocode the point
3. Determine if the point is on land or water by checking to see if the point has a valid address
• If on water, increment waterCount
• If on land, determine the country/region of the point, and add it to the countryFrequencies dict.

Try reading the actual code with the pseudocode for yourself!

Challenge #1: GeocoderTimedOut

My programme worked, but it was still quite slow, reverse geocoding 1 coordinate at a time. I would test over 500 coordinates (which I shall hereafter refer to as "trials"), but I kept getting this error:

raise GeocoderTimedOut('Service timed out')
    geopy.exc.GeocoderTimedOut: Service timed out

Moreover, at one point, I realised that this process was I/O bound and so I could improve the speed by multithreading, but then the GeocoderTimedOut error only got worse.

I researched a lot about this and found a few solutions:

• Implementing a recursive function and setting a Try/Except/Finally to catch the error
• Adding the timeout= attribute to the reverse geocoding call
• And some more dubious ones...

In the end I wrote a recursive function reverseGeocode() with error handling and removed multithreading. It works most of the time, but sometimes it gets stuck in an infinite GeocoderTimedOut loop.

Challenge #2: KeyError

The next challenge I faced was a mysterious KeyError. With a lot of debugging with print() statements, I found out that Antarctica has an address but not a country property, so when I was trying to access the country of the coordinate with country = location.raw["address"]["country"] , it gave me a KeyError. Therefore, I simply added a Try... Except KeyError to catch this special case.

Sample Output

Results

I conducted 10 trials each for 20, 100, 200, 300 and 500 images. Here are the results:

No. trials	% of water found on the Earth
	Trial 1	Trial 2	Trial 3	Trial 4	Trial 5	Trial 6	Trial 7	Trial 8	Trial 9	Trial 10	Mean
20	60.0	65.0	75.0	65.0	75.0	75.0	75.0	85.0	65.0	50.0	69.00
100	67.0	78.0	72.0	62.0	69.0	79.0	63.0	79.0	72.0	75.0	71.60
200	76.5	69.0	69.5	73.5	74.5	70.5	71.0	72.0	71.0	73.0	72.05
300	71.0	72.3	69.3	68.7	71.7	70.0	70.7	71.3	72.0	72.3	70.93
500	71.0	69.2	73.2	71.2	70.8	72.0	70.4	70.2	70.8	72.0	71.08

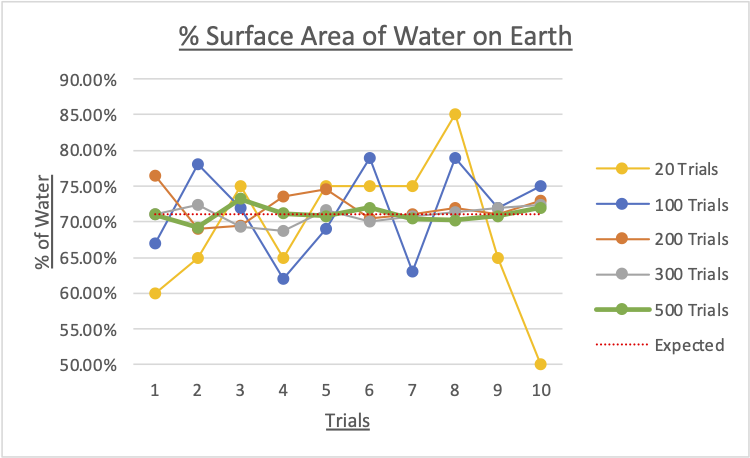
According to the Oceanic Institute of the Hawaii Pacific University, the oceans account for 71% of the Earth’s surface area.

Surprisingly, the mean with 100 trials - $71.60\%$ - was quite accurate, but it must be noted that it has a high range of $17\%$ from $62.0\%$ to $79.0\%$, suggesting a high uncertainty of the data.

In contrast, with 300 trials, the mean is $70.93\%$ and the range is only $3.6\%$ from $68.7\%$ to $72.3\%$.

From the graph above, 200 trials will give you enough precision in order to be confident you were close to the actual percentage. There appears to be no significant difference between 300 and 500 trials.

Obviously, this method cannot account for inland bodies of water such as lakes, rivers, and ponds. However these sources are mostly negligible considering the relative size of the oceans and the inherent error of this method.