As I was looking at some STEP questions for the Cambridge admissions test for mathematics, I came upon something which piqued my interest: the Stirling's approximation. This is essentially an approximation for $n!$ which is accurate even for small values of $n$. Naturally, I researched about it, and found that the derivation involves some interesting calculus which I wanted to showcase in today's post.
I have taken the proof from mostly this Wikipedia article, but I have expanded on it by reading other sources to make the mathematics easier to understand. In addition, instead of using the Euler-Maclaurin formula and the Bernoulli numbers, I used an alternative method.
The neat trick to approximate factorials involves taking the natural logarithm of a factorial and using the log laws to simplify it into a sum of natural logarithms. For example, to approximate $N!$, $$\ln(n!)=\ln(n(n-1)(n-2)...2*1)=\ln(n)+\ln(n-1)+...+\ln(2)+\ln(1)$$
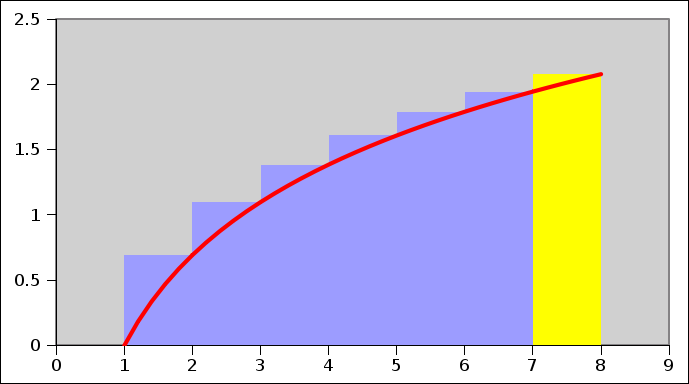
The right hand side can now be expressed as an integral, $$\ln(n!)=\int_1^n{\ln(x)}$$
Now, since $\ln{x}$ is a monotonically increasing function over the interval $(0, \infty)$, we can bound the integral as follows:
$$
\int_{n-1}^{n}{\ln{x}dx}<\ln{x}<\int_{n}^{n+1}{\ln{x}dx}
$$
If we add this above equality for $n=1,2,3,4...N$, we get:
$$
\int_{0}^{N}{\ln{x}dx}<\ln{N!}<\int_{1}^{N+1}{\ln{x}dx}
$$
using the fact that $$\ln(N!)=\ln(1)+\ln(2)+...+\ln(N-1)+\ln(N)$$ as we previously showed.
Now we can integrate both bounds. As I'm sure you know already, to evaluate $\int_{1}^{n}\ln{x} dx$, we can use a neat trick of "multiplying by 1" in order to use integration by parts where $u=\ln{x}$ and $dv=1$ so that $du=\frac1x$ and $v=x$.
$$
\begin{aligned}
\int\ln(x)dx&=x\ln{x}-\int{x\cdot\frac1xdx}
\\ &=x\ln{x}-x+C
\end{aligned}
$$
Since $\ln{0}$ is undefined, the left integral is improper, but we can easily solve that by using an arbitrary variable and taking the limit:
$$
\begin{aligned}
\int_{0}^{N}{\ln{x}dx}&=\lim_{t \to 0}\int_t^N{\ln{x}dx}
\\ &=\lim_{t \to 0}[({N\ln{N}-N})-(t\ln{t}-t)]
\\ &=N\ln{N}-N
\end{aligned}
$$
So, the inequality becomes
$$
N\ln{N}-N<\ln(N!)<(N+1)\ln{(N+1)-N}
$$
Now here is where things get tricky. We will define
$d_n=\ln{n!}-(n+\frac12)\ln{n}+n$
So,
$$
\begin{aligned}
d_{n+1}&=\ln{((n+1)n!)}-(n+\frac32)\ln{(n+1)+n+1}
\\ &= \ln{(n+1)}+\ln{n!}-(n+\frac32)\ln{(n+1)+n+1}
\\ &= \ln{n!}-(n+\frac12)\ln{(n+1)}+n+1
\end{aligned}
$$
Therefore,
$$
\begin{aligned}
d_n-d_{n+1}&=[\ln{n!}-(n+\frac12)\ln{n}+n]-[\ln{n!}-(n+\frac12)\ln{(n+1)}+n+1]
\\ &=(n+\frac12)\ln{(n+1)}-(n+\frac12)\ln{n}-1
\\ &=(n+\frac12)\ln({\frac{n+1}{n})}-1
\end{aligned}
$$
Now we want to simplify the $\ln({\frac{n+1}{n})}$ term using Taylor series:
$$
\begin{aligned}
\ln\Big({\frac{n+1}{n}\Big)}&=\ln{(n+1)}-\ln{n}
\\ &=\ln{(n+1)}+\ln{2}-\ln{2}-\ln{2}
\\ &= \ln{(2n+2)}-\ln{(2n)}
\\ &= \ln{(2n+2)}-\ln{(2n+1)}+\ln{(2n+1)}-\ln{(2n)}
\\ &= \ln{\frac{2n+2}{2n+1}}-\ln{\frac{2n}{2n+1}}
\\ &=\ln{(1+\frac{1}{2n+1})}-\ln{(1-\frac{1}{2n+1})}
\\ &\text{Now, using the Taylor series expansion for } \ln{(x+1)},
\\ &=\sum_{k=1}^{\infty}(-1)^{k-1}\frac{1}{k}\Big(\frac{1}{2n+1}\Big)^k \ - \Bigg(-\sum_{k=1}^{\infty}\frac{1}{k}\Big(\frac{1}{2n+1}\Big)^k\Bigg)
\\ &\text{The series telescopes. Even terms cancel, odd terms double}
\\ &=2\sum_{k=0}^{\infty}\frac{1}{2k+1}\Big(\frac{1}{2n+1}\Big)^{2k+1}
\end{aligned}
$$
Therefore,
$$
\begin{aligned}
d_n-d_{n+1}&= (n+\frac12)\ln\Big({\frac{n+1}{n}\Big)}-1
\\ &=(n+\frac12)2\sum_{k=0}^{\infty}\frac{1}{2k+1}\Big(\frac{1}{2n+1}\Big)^{2k+1}-1
\\ &=(2n+1)\sum_{k=0}^{\infty}\frac{1}{2k+1}\Big(\frac{1}{2n+1}\Big)^{2k+1}-1
\\ &=\sum_{k=1}^{\infty}\frac{1}{2k+1}\Big(\frac{1}{2n+1}\Big)^{2k}
\\ &>0
\end{aligned}
$$
Therefore, $d_n>d_{n+1}$, so the sequence $d_n$ is monotonically decreasing which means that $\frac{1}{2k+1}<1.$ So, we can remove this factor and introduce an inequality:
$$
d_n-d_{n+1}<\sum_{k=1}^{\infty}(\frac{1}{2n+1})^{2k}
$$
This is an infinite geometric series with first term $=\frac{1}{(2n+1)^2}$ and common ratio also $=\frac{1}{(2n+1)^2}$
$$
\begin{aligned}
&=\frac{\frac{1}{(2n+1)^2}}{1-\frac{1}{(2n+1)^2}}
\\ &=\frac{1}{4n(n+1)}
\end{aligned}
$$
Rewriting with partial fractions,
$$
=\frac{1}{4n}-\frac{1}{4(n+1)}
$$
which means the sequence is bounded by $\frac14$, so $d_1-d_n<\frac14$ (remember, we want $d_1-d_n$ and not $d_n-d_1$ because we previously proved that the sequence $d_n$ is monotonically decreasing).
Therefore, $d_n>d_1-1/4$, which means that $d_n$ is bounded below.
Finally, we invoke the Monotone Convergence Theorem in the case of a decreasing sequence to conclude that $d_n$ converges to its infimum. Let this value be $C$. Then, we can simply exponentiate $d_n$ to get: $$ \begin{aligned} \lim_{n \to \infty}d_n&=C \\ \lim_{n \to \infty} e^{\ln{n!}-(n+\frac12)\ln{n}+n}&=e^C \\ \lim_{n \to \infty} \frac{n!e^n}{n^{(n+1/2)}} &= e^C \end{aligned} $$ We can rewrite this in a more "beautiful" form by using the asymptotic symbol, $\sim$, which means that their "ratio tends to 1 as $n \to \infty$: $$n! \sim e^C\sqrt{n}\Big(\frac{n}{e}\Big)^n$$ Almost done. We now have to find the value of $e^C$. To do this, we will use the Wallis product, which states that: $$ \begin{aligned} {\frac {\pi }{2}} &= \prod _{n=1}^{\infty }{\frac {4n^{2}}{4n^{2}-1}}=\prod _{n=1}^{\infty }\left({\frac {2n}{2n-1}}\cdot {\frac {2n}{2n+1}}\right) \\&={\Big (}{\frac {2}{1}}\cdot {\frac {2}{3}}{\Big )}\cdot {\Big (}{\frac {4}{3}}\cdot {\frac {4}{5}}{\Big )}\cdot {\Big (}{\frac {6}{5}}\cdot {\frac {6}{7}}{\Big )}\cdot {\Big (}{\frac {8}{7}}\cdot {\frac {8}{9}}{\Big )}\cdot \;\cdots \\ \end{aligned} $$ Proving this requires the use of the Wallis integral and the squeeze theorem which is a topic for another day. For this part, the proof wiki page is quite easy to understand:
Substituting $n! \sim a\sqrt{n}\Big(\frac{n}{e}\Big)^n$,
Note: the above proof uses $n! \sim a\sqrt{2n}\Big(\frac{n}{e}\Big)^n$, which is why we get $\sqrt{x}$ instead of $\sqrt{2x}$.
Since we have shown that $e^C = \sqrt{2\pi}$, we can now finally state the Stirling formula: $$n! \sim e^C\sqrt{2\pi n}\Big(\frac{n}{e}\Big)^n$$
There is a much faster, but arguably more advanced, derivation using what is known as the Laplace's method. As this post is already very long, I will not include it here, but go take a look here!
Phew, that was very long! (and very long for me to type, too...) To summarise, the proof required a multitude of techniques: taking the logarithm and rewriting an infinite product as an infinite sum, expressing as an inequality, improper integrals, Taylor series, infinite geometric series, the Monotone Convergence Theorem and of course, the Wallis product.
